Optimisation
Lorsqu'on l'entraîne, un système d'apprentissage automatique présente une courbe d'apprentissage qui fait le lien entre les erreurs et les paramètres d'ajustement. Cette courbe est une fonction de perte ou de coût (loss function) et se présente souvent comme une fonction graphique convexe.
Qu'est-ce que cela signifie ? Chez l'humain, un processus d'apprentissage peut se représenter comme une fonction en « S », avec une phase initiale, une phase d'accélération (l'apprentissage en action) et une phase de maturation (l'optimum). Ainsi, on ne peut pas dire qu'on apprend « trop », il n'y a pas de phase descendante. Une fois qu'on a appris quelque chose, on le sait (ou alors on l'oublie, mais c'est un autre processus).
Avec les machines, c'est différent. Il y a deux manières d'approcher une phase d'optimum, soit en restant en deçà soit en restant au-delà. Si l'optimum est un seul point d'apprentissage (un instant \(t\) d'activation), alors tout l'enjeu est de savoir comment l'atteindre soit en augmentant soit en diminuant quelque chose. Ainsi, on ajuste les paramètres du modèle à chaque itération jusqu'à ce que le modèle produise un résultat qui convient. On comprend pourquoi il faut automatiser cet apprentissage : il s'agit de mettre en place un ou plusieurs algorithmes d'optimisation qui ajustent les paramètres selon une méthode répétée à chaque fois.
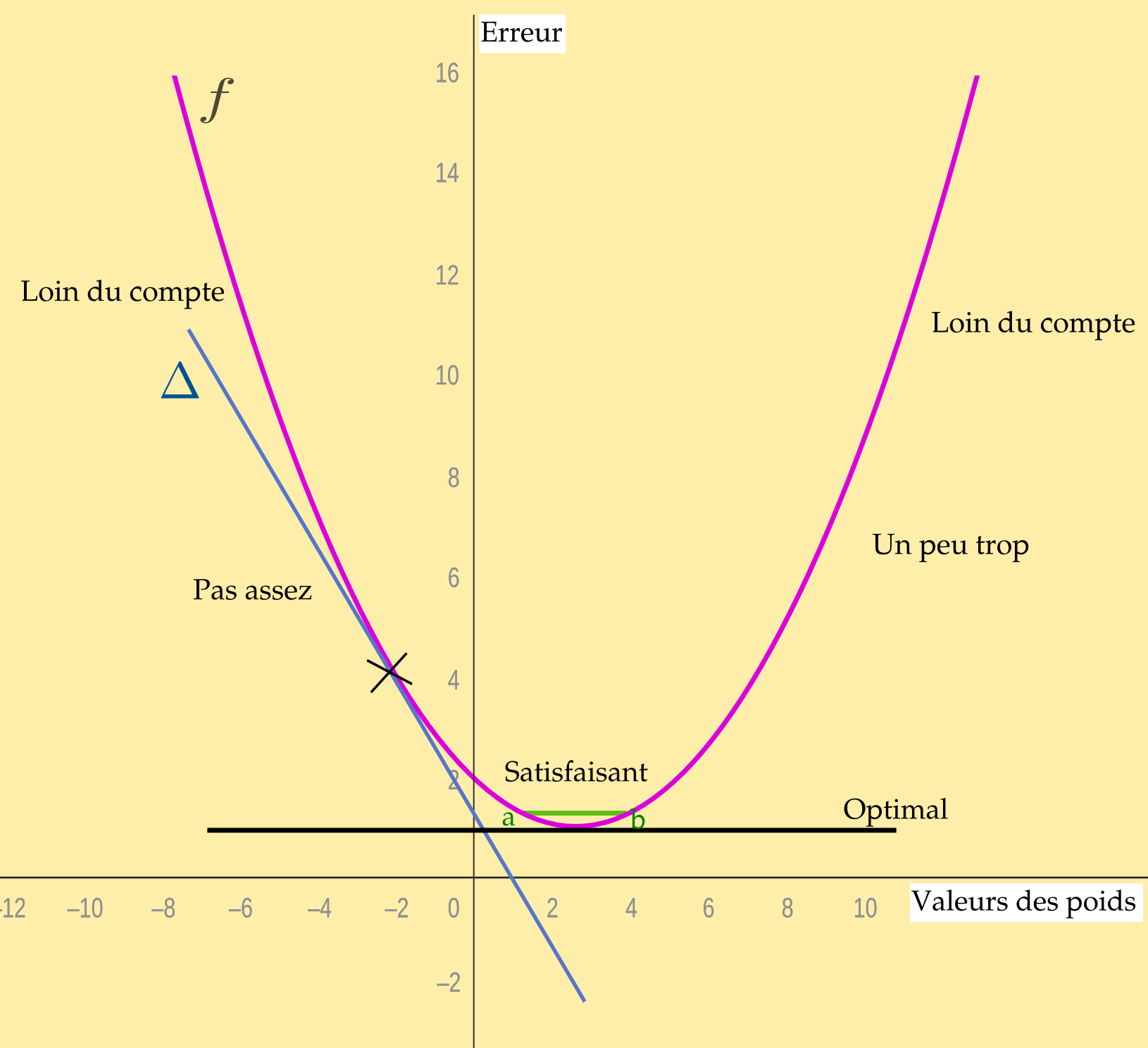
On peut représenter la fonction de coût : c'est une courbe en « U », une fonction convexe. Pourquoi ? parce qu'elle nous permet de considérer l'apprentissage, c'est-à-dire les valeurs des poids, en fonction des erreurs constatées. Ensuite, par une méthode de descente de gradient (cf ci-dessous), on cherche à savoir comment nous rapprocher de l'optimum (le point le plus bas). Une telle fonction présente un minimum global (et pas plusieurs minima locaux qui pourraient nous fourvoyer). Ainsi quel que soit le point où l'on commence à mettre en oeuvre la descente de gradient, on ne peut que converger vers cet optimum. La mise à jour des calculs (selon les itérations) permet de stabiliser les paramètres car la trajectoire est prévisible1.
Bien entendu, ce que nous produisons ci-dessous est une représentation simplifiée du système. Les « valeurs » des poids ou les erreurs ne se présentent jamais en une seule image d'une fonction.
Ce qu'on veut, c'est se rapprocher le plus possible d'une valeur optimale, celle dont on pourrait être certain qu'elle sera la même à chaque fois. Comme le système d'IA ne donnera jamais que des valeurs plus ou moins proches de cette valeur idéale (le résultat attendu), l'idée est d'optimiser sa courbe d'apprentissage, c'est-à-dire trouver les meilleurs valeurs de paramètres qui permettent de se rapprocher voire d'atteindre l'optimum (le moins d'erreur possible).
On voit bien ici qu'il s'agit d'un système tout différent que si nous donnions au calculateur à la fois les données et un programme. Dans ce cas, un mauvais résultat n'est jamais une erreur de calcul mais une erreur de programme. Par contraste, dans un système d'apprentissage automatisé, si le résultat ne convient pas, c'est que le système doit encore s'entraîner ou que le jeu de données de départ n'est pas suffisant ou mal construit.
Pour optimiser un modèle, il faut agir sur son taux d'apprentissage, c'est-à-dire les pas qu'il faut franchir en pente vers l'optimum en réduisant les erreurs. L'une des méthodes algorithmiques utilisées pour cela est la descente de gradient. À chaque itération durant la phase d'apprentissage on effectue un chemin inverse (par rétropropagation) dans le réseau en s'intéressant à chaque poids, à chaque condition des fonctions d'activation des neurones.