Naissance d'un modèle

Information

Cette section cherche à illustrer en un seul jet les concepts techniques que nous avons vu précédemment.

Pour expliquer ce qu'est un réseau de neurones (artificiels), imaginons une machine sur le modèle du Perceptron de Frank Rosenblatt (1957). Sauf que nous allons la simplifier pour obtenir ce qu'on appelle une combinaison linéaire, c'est-à-dire des entrées, une couche neuronale unique avec une seule fonction neuronale, et une sortie. En d'autres termes, c'est ni plus ni moins qu'un problème à plusieurs facteurs que vous pouvez parfaitement résoudre « à la main » en faisant des moyennes. Tel est le cas que nous allons aborder en première partie, dans ce qu'on appelle la propagation vers l'avant du réseau, c'est-à-dire une méthode de traitement de l'information pour obtenir une sortie.

Nous verrons ensuite les limites de ce modèle simplifié et pourquoi il est intéressant d'aller un peu plus loin. En seconde partie nous verrons comment un tel modèle peut se doter de fonctions d'apprentissage, grâce à une méthode « à rebours », une propagation vers l'arrière, en soumettant au modèle des exemples dont nous connaissons déjà la sortie.

Premier mouvement : propagation vers l'avant

Attention

En prenant le cas imaginaire d'une recherche d'appartement selon des critères de choix, nous allons décrire un modèle décisionnel simpliste qui n'a absolument aucun intérêt à être automatisé. Nous verrons en revanche que la complexité des critères peut être décrite à la manière d'un système d'IA afin de comprendre comment des coefficients de pondération peuvent jouer dans un modèle connexionniste.

Dans notre cas, imaginons que vous voulez acheter un appartement et que, selon quatre critères, vous souhaitez décider de son achat. Votre premier critère sera la différence entre le prix annoncé et le prix moyen au \(m^2\) dans la ville (\(c_1\)), le second critère sera le nombre de bars dans le quartier (\(c_2\)), le troisième la distance du plus proche arrêt de bus (\(c_3\)), et le quatrième la consommation énergétique annuelle de l'appartement (\(c_4\)). Une fois que vous avez rassemblé vos renseignements, vous allez accorder un poids sur une échelle de \(-1\) à \(+1\) pour chacun de ces critères en fonction des valeurs que vous avez trouvées. Tout cela est très subjectif, nous sommes d'accord.

Plus concrètement, une fois qu'on a indiqué des valeurs pour chacun des critères, indépendamment des unités (euros, Kwh, mètres, etc), on les pondère par rapport à l'importance relative que chaque critère entretien avec les autres. Par exemple :

Critère	Valeur	Cœfficient de pondération
Prix au \(m^2\)	3700	0,9
Distance arrêt de bus	350	0,5
Nombre de bars	2	0,3
Consommation énergétique	9000	0,8

Ces valeurs sont relatives à autant de poids (\(w\)) de chaque critère, c'est à dire « combien elles comptent » dans l'équation. Sont-elles importantes, primordiales, secondaires, négligeables ? Dans notre exemple, si nous attribuions le même poids ou coefficient à chaque critère, cela reviendrait à tous les mettre sur le même plan. Rien n'empêche de leur attribuer des coefficients différents, ainsi ils ne pèseront pas tous de la même manière dans notre balance. La pondération est une composante nécessaire des modèles d'IA, c'est par le jeu de pondération qu'un réseau neuronal fini par prendre sa forme opérationnelle.

Au bout du compte, nous recherchons une valeur \(y\) pour chaque logement étudié. Ici, c'est le niveau d'acceptabilité de l'achat.

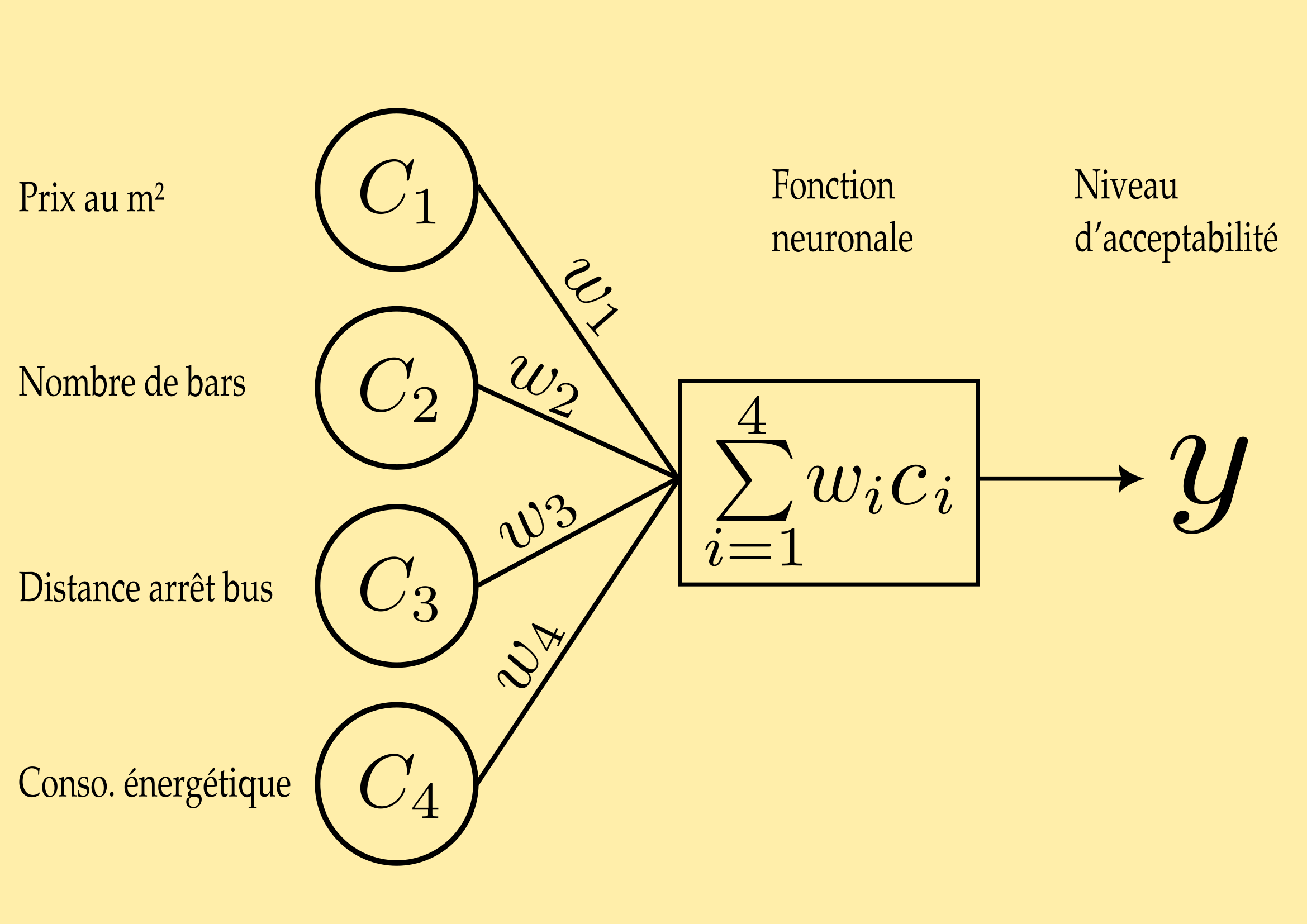
Calculateur à couche neuronale unique

La fonction neuronale du calculateur que nous avons créé consiste donc à effectuer la somme pondérée des critères choisis :

\(\sum_{i=1}^4 w_ic_i = w_1c_1 + w_2c_2 + w_3c_3 + w_4c_4\)

Ce que nous venons de faire revient à systématiser une décision que nous pouvons très bien faire de tête en un rien de temps ! En effet, si vous avez trois appartements à comparer uniquemement selon ces critères, vosu prendrez bien vite votre décision. Il suffit pour cela que vous sachiez quel poid accorder à quel critère dans la balance. Seulement, si vous étiez une machine il faudrait vous entraîner des centaines et des centaines de fois, sur ces milliers de données (disons carrément toute l'offre immobilitère locative française des 10 dernières années) pour trouver le meilleur rapport des coefficients de pondération pour le meilleur choix possible.

Ensuite, un peu plus abstrait, il s'agit d'attribuer des biais.

C'est-à-dire que pour chaque entrée, nous avons vu que le réseau associe un poids (\(w\)). Mais celui-ci peut être relatif aux biais que vous souhaitez implémenter dans le modèle. Par exemple, si vous recherchez un quartier calme le soir, le fait qu'il n'y ai qu'un seul bar n'est pas forcément pertinent (il peut être situé juste dans votre rue). Dès lors pour \(c_2\), vous pouvez ajouter un biais selon lequel, par exemple, si le nombre de bars est supérieur à 3, alors \(w_2\) est multiplié par 5. Notez pour la suite : ce biais est appelé \(b\).

Remarquez que ce n'est pas la même chose que le poids : ici, c'est un facteur multiplicateur « en surplus » du système.

Jusque là ça va ? Intéressons-nous un peu à la valeur de sortie, c'est-à-dire \(y\). Il s'agit d'une valeur qui est censée éclairer votre choix. Il faut donc en déterminer un seuil. Disons que si \(y\) a une valeur supérieure ou égale à ce seuil, nous pouvons affirmer que l'appartement peut être choisi. Si la valeur de \(y\) est inférieure, alors nous passons à l'étude d'un autre appartement.

si \(\sum_{i=1}^4 w_ic_i +b \geq 0\), alors la sortie est positive
si \(\sum_{i=1}^4 w_ic_i + b < 0\), alors la sortie est négative

Et là, vous allez dire : « bof ». Tout ça c'est bien joli, mais cela reste binaire. Hé oui, c'est parce que notre modèle est en fait très limité. Par exemple, si un appartement est très beau et chaleureux, vous pourriez être prêt à sacrifier l'un des critères que vous appliquez aux autres appartements au profit de ce critère d'esthétique. Comment faire pour que ce critère puisse tout de même entrer en ligne de compte pour certains appartements et pas d'autres ? Et puis, après tout, il y a tellement d'autres critères de choix : l'état de rénovation à prévoir, la couleur des murs du hall d'entrée, la luminosité, la proximité du marché, etc.

Compliquons un peu les choses

Pour obtenir un système qui nous permettra d'obtenir la décision finale à partir de multiples conditions de poids à chaque couche décisionnelle (chaque noeud de connexion), il faut :

passer à un modèle supérieur avec d'autres groupes de critères ;
intégrer des fonctions d'activation qui conditionnent les rapports entre les poids et l'état d'activation des neurones ;
comprendre qu'un neurone peut ou pas être activé en fonction de l'activation d'autres neurones avant lui et pas uniquement en fonction de critères d'entrée dans le système : il y a d'autres couches neuronales.

Nous allons donc donner une autre forme à notre modèle. Nous allons multiplier les critères et les considérer comme des groupes de critères à l'entrée du modèle. Chaque critère entre en « relation » avec d'autres sur la base du résultat du calcul de \(\sum_{i=1}^n w_ic_i +b\) que nous pouvons noter \(z\) et d'une fonction dite d'activation. Cette fonction d'activation indique comment le neurone est connecté : cela peut être binaire (\(0\) ou \(1\)), mais celaa peut être aussi un ensemble de valeurs qui font que dans certains cas il sera activé et pas dans d'autres.

Les couches cachées sont les couches de traitement de l'information selon des « genres ». pour notre besoin de choix d'appartement, nous pouvons dire :

que la couche \(z_1\) concerne le traitement d'entrée (c'est-à-dire la couche unique de notre modèle précédent),
que la couche \(z_2\) concerne les coûts induits par rapport aux poids des critères (par exemple si la consommation énergétique est élevée, il faut envisager une rénovation de l'isolation, si la valeur de l'esthétique est basse, il faut envisager de refaire la décoration intérieure, etc.). On peut imaginer des échelles de dépenses à envisager en fonction des connexions (et des poids) précédents (par exemple des palliers en milliers d'euros: 10, 20, 30, 100).
et la couche \(z_3\) met tout cela en relation avec les taux d'emprunt selon les banques du quartier, les assurances, l'âge du capitaine, etc.

C'est cela les fonctions d'activation : il s'agit de déterminer les seuils qui vont activer ou pas nos neurones.

Par exemple, un critère esthétique comme la couleur des murs n'a pas vraiment de poids par rapport aux critères énergétiques comme la consommation de gaz. Dès lors, il n'influera que peu voire pas du tout sur l'activation neuronale qui connecte à la fois les groupes esthétique et énergie, à moins de lui imposer un biais particulièrement fort.

Autre exemple : s'il n'y a pas de bus à proximité, ce poids va influer sur les coûts induits (comme ceux liés à l'achat d'une voiture ou d'un vélo), et si cette absence de bus à proximité fait augmenter drastiquement les coûts induits de la dépense énergétique liée à l'achat de l'appartement (en \(z_2\)), comme les dépenses de carburant pour votre voiture, il influencera par voie de conséquence le critère de choix qui repose sur le nombre d'achats futurs à prévoir et peut-être l'importance des emprunts bancaires à prévoir (en \(z_3\)), comme l'achat d'une voiture ou d'un vélo électrique.

Encore en d'autres termes, les couches \(z\) sont les couches neuronales dont les fonctions d'activation sont déterminées par les poids synaptiques des sorties précédentes. En \(z_1\) nous avons le traitement de l'information brute, et en \(z_n\) autant de « sous-traitements » qu'il faut pour déterminer une sortie finale. Quant au poids synaptique, c'est lui qui va déterminer si la connexion neuronale est plus ou moins forte, cela aura toute son importance lorsque nous allons traiter de l'apprentissage en seconde partie.

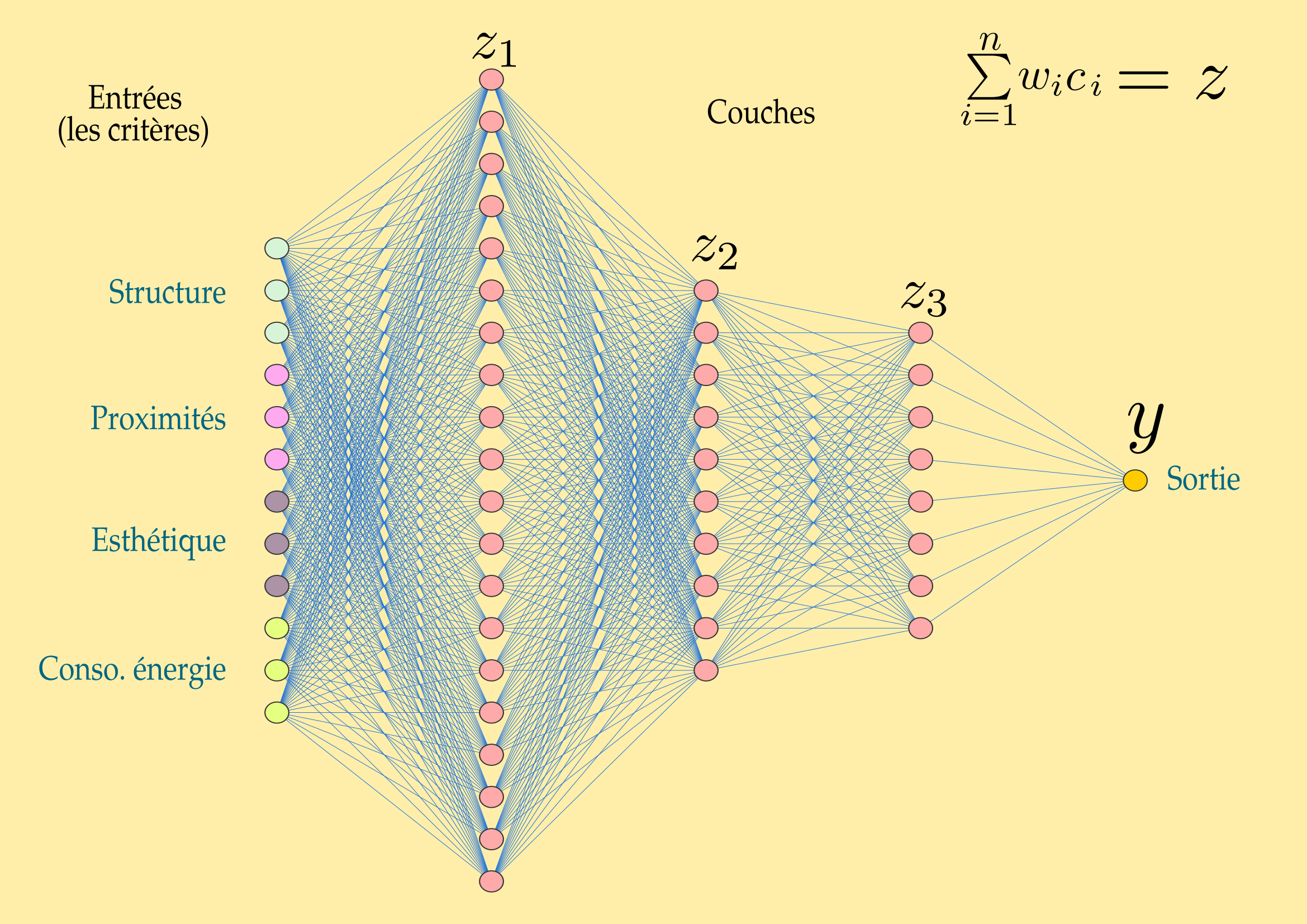
Calculateur muti-couches

Évidemment, notre modèle reste encore très simplifié. Entre les couches \(z_2\) et \(z_3\) il faut envisager des sous-couches, des arbres décisionnels qui vont permettre de déterminer encore d'autres valeurs, etc.

Vous suivez toujours ?

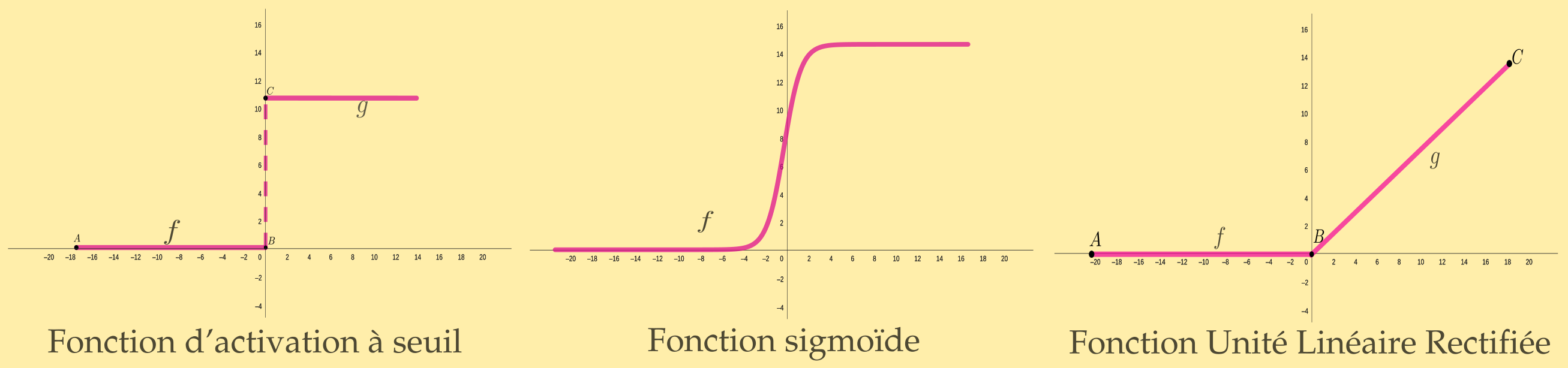
La fonction d'activation, elle, est l'une des multiples fonctions d'activation des modèles de neurones artificiels. En effet, il faut encore se demander à partir de quand (quel seuil) le neurone est censé être activé. On peut donner trois types de fonctions (il y en a d'autres) pour comprendre comment un modèle neuronal peut réagir :

La première est une fonction step, c'est la plus simple : un neurone s'active une fois le seuil franchi. C'est un comportement binaire comme dans notre premier modèle : soit \(0\) soit \(1\). Cette fonction est linéaire. Les deux fonctions suivantes permettent d'approcher beaucoup plus finement le shéma décisionnel.
La seconde est une fonction sigmoïde : le seuil d'activation est à définir sur un intervalle. Par exemple \(\sigma(z)=\frac{1}{1+e^{-z}}\). Si le point zéro est le point de basculement, ce n'est pas très important, car tout est question de savoir si le neurone est peu activé ou très activé et à partir de quand il commence à pencher d'un côté ou de l'autre. On constate aussi que plus les valeurs sont éloignées, plus la pente est faible, et moins le poids à d'importance en positif comme en négatif.
La troisième, c'est la fonction ReLU (Rectified Linear Unit, unité linéaire rectifiée), \(R(z)=max(0,z)\). En fait, cette fonction n'est linéaire que sur un intervalle, mais celui ci a la particularité de n'être que du côté positif. C'est-à-dire que l'activation ou la désactivation d'un neurone n'est jamais qu'une question d'écriture : en dessous de zéro, rien de change, au dessus les valeurs changent de manière linéaire en fonction des poids d'entrée. La fonction ReLU (et ses variantes) est l'une des plus utilisées car, étant donné que les valeurs de désactivation sont « mortes », elle permet une meilleure approche de la backpropagation, c'est-à-dire la correction des gradients, qui ne cherche donc pas à corriger ces valeurs « mortes ». Et ceci fait une excellente transition vers notre seconde partie.

Propagation vers l'arrière

(… ou : comment on fait de l'apprentissage)

Nous avons parlé plus haut de poids synaptiques ou de coefficients synaptiques. Arrêtons-nous un instant sur la signification de cette expression. Dans les années 1940, les premières recherches sur la formalisation logique du système neuronal biologique considéraient les neurones comme de simples portes ouvertes ou fermées. On savait bien sûr que les connexions neuronales se faisaient par les synapses, une zone de contact entre deux neurones. Mais c'est plus tard qu'on a découvert que plus la connexion synaptique entre deux neurones est forte, plus elle est durable dans le temps, mais on a découvert aussi que ces connexions ne sont pas figées et peuvent s'enrichir par apprentissage : se renforcer ou au contraire se détendre au profit d'autres connexions.

Là s'arrête l'analogie avec le cerveau humain. Dans le cas d'une machine, implémenter l'apprentissage revient à trouver les meilleures connexions synaptiques entre les neurones de manière à prédire un résultat. C'est-à-dire qu'il s'agit d'inventer une machine qui ne servira pas à traiter un seul type d'information, mais tout type d'information dont le traitement peut-être assuré par une plasticité neuronale susceptible de mettre à profit ce que la machine a appris pour donner une réponse. Autrement dit, l'apprentissage se fait en analysant un nombre gigantesque de données, et le nombre de connexions est lui aussi gigantesque. Plus rien à voir avec le modèle simpliste dont nous parlions plus haut ! Si les principes sont les mêmes, il va faloir ajouter encore deux ou trois choses.

Comment la machine peut-elle apprendre ? Il n'y a pas beaucoup de solutions : il faut présenter des données d'entrées et poser une question dont on connnait déjà la réponse pour la comparer avec celle que nous donne la machine. Si la réponse donnée ne correspond pas à la réponse attendue, l'un des premiers travaux consiste à modifier les coefficients synaptiques (et identifier lesquels), c'est-à-dire effectuer la démarche à rebour du système, soit un chemin propagatoire vers l'arrière (back propagation). On pourra aussi, évidemment, multiplier encore les couches si besoin, ou implémenter des biais.

Pour ce faire, l'idée consiste à employer une main d'oeuvre peu chère, c'est-à-dire des esclaves, si possible sans avantages sociaux, de manière à explorer les connexions une à une en cliquant en longueur de journée sur des indicateurs… Non ! Quoique cette plaisanterie n'est pas si fantasque que cela car les machines ne savent pas encore tout faire toutes seules.

Ce que nous allons voir à partir de maintenant, c'est encore de la théorie et des principes. Ils permettent de bâtir des IA, mais il faut garder en tête que les données d'entrées sont parfois étiquetées de manière à donner des indicateurs dans le processus d'apprentissage automatique (on parle d'apprentissage semi-automatique, ou supervisé). Et cet étiquetage, il faut parfois des petites mains pour le faire…

Encore une précision. Ici nous parlons de modèles d'IA classiques, c'est-à-dire destinés à un usage particulier, pour faciliter la compréhension. Les modèles plus larges, entraînés sur des schémas, des structures et des représentations glaobaux, sont des modèles de fondation. Ce n'est pas notre sujet ici.

Apprendre

Pour entraîner une machine, il nous faut des jeux de données de deux sortes : des données d'entrées et des données de validation. Et il faut faire correspondre ces entrées et ces validations en comparant avec les prédictions du modèle. Oui, parce qu'une IA prédit : d'une part elle analyse des grands jeux de données et donne un résultat probable ou probant, et comme cela est complexe (il y a un grand nombre d'interactions) elle permet d'anticiper une décision (ici, l'achat d'un appartement).

Donc le modèle réussi en cas de correspondance. Il a la bonne valeur \(y\) en sortie. Dans notre cas, il s'agit d'entrer des valeurs pour lesquelles nous jugeons que \(y\) est faible ou fort, c'est-à-dire qu'on va utiliser plein de combinaisons de critères pour lesquelles nous savons que l'appartement est un mauvais choix et d'autres combinaisons pour lesquelles nous savons qu'il est un bon choix. Comme on peut s'y attendre, à l'extrêmité des valeurs de ces combinaisons, c'est assez facile à prédire : une consommation énergétique délirante, un nombre de bars improbable, etc. Là où cela se complique, c'est lorsqu'on fait jouer des entrées plus fines. Mais c'est là que cela devient intéressant.

Il nous faut encore des maths… En effet, il n'est pas humainement possible de vérifier chaque chemin et chaque poids pour chaque correspondance entre les entrées et les sorties. C'est pourquoi on parle d'apprentissage automatique.

La première étape consiste donc à minimiser les erreurs, c'est-à-dire vérifier quand le modèle nous sort n'importe quoi, et quand il se rapproche des bonnes valeurs d'entraînement.

Pour déterminer cela, nous allons utiliser une fonction de coût (ou peut dire aussi fonction de perte). C'est une fonction qui quantifie l'écart (les erreurs) entre une prédiction du modèle et les valeurs attendues des données d'entraînement. Dans les milieux initiés, on appelle généralement cet écart \(\hat{y}\) (y - hat).

Pour coller à notre étude de cas du choix d'un appartement selon des critères d'entrée, imaginons que nous ayons à disposition une vaste étude socio-démographique où nous pouvons déterminer ces critères par rapport à des milliers de personnes qui ont acheté un appartement ces 5 dernières années. L'idée consiste donc à tester pour chaque critère d'entrée les bonnes valeurs de sortie par rapport aux choix effectués par tous ces gens, c'est-à-dire les coefficients relatifs aux critères de choix et à leurs impications : qu'est-ce qui conditionne les montants empruntés, les contraintes de la rénovation à envisager, bref toutes les couches \(z\) dont les connexions neuronales déterminent le modèle décisionnel qui sera dessiné à l'issue de l'entraînement.

…Mais à ce stade, notre machine n'apprend toujours rien ! On n'a fait que constater ses erreurs. Il faut aller un peu plus loin avec cette histoire de courbe.

Descente de gradient

Qu'en est-il des poids, ces coefficients synaptiques ? Au départ, ils sont attribués de manière subjective, en fait. Ce qu'on veut, c'est les faire jouer pour que le modèle puisse trouver les bons chemins synaptiques durant son apprentissage. Mais faut-il les augmenter ? si oui, lesquels ? faut-il les diminuer ? si oui, lesquels ?

Vous vous souvenez peut-être d'avoir un jour tracé une droite au milieu d'un nuage de points dans un repère. On vous a parlé de régression et de statistiques… Et on vous a demandé pour cela de tracer la droite d'ajustement, ou fonction affine. Celle qui ressemble à \(f(x) = (x-n)^2\). Pour tracer cette droite on peut la faire passer au « milieu » du nuage de points en calculant le point moyen, utiliser la méthode des moindres carrés, ou encore d'autres méthodes. Imaginez que ces points représentent les différentes valeurs d'entraînement, les valeurs des poids synaptiques, les \(x\). L'idée est d'approcher au mieux les valeurs qui fonctionnent le mieux. Sauf que nous sommes dans une mesure d'écart où il va nous faloir savoir quand il faut activer (ou plus ou moins activer) le neurone.

Or, on ne peut pas se contenter d'une droite car chaque point doit relater à la fois à l'erreur (ou la perte) \(ŷ\) et le poids concerné. C'est une courbe qu'il nous faut. La fonction doit être convexe, avec un point de convergence, en bas, qui est le point d'activation proprement dit, les autres points étant des valeurs qui s'éloignent ou se rapprochent du « bon » point.

Cette courbe, c'est la fonction qui illustre l'écart entre la valeur \(y\) de sortie et le résultat attendu. En abscisses nous avont les valeurs des poids synaptiques, en ordonnées les valeurs d'erreur (la perte ou le coût). La fonction est du genre \(J(\theta)=(\theta-n)^2\) (pour utiliser les bonnes conventions de lettres).

(Bien entendu, ce que nous produisons ici est une représentation simplifiée, schématique, du système. Les « valeurs » des poids ou les erreurs ne se présentent jamais en une seule image d'une fonction.)

L'objectif n'est pas seulement de savoir où on se situe sur la courbe mais de savoir s'il faut monter ou descendre, s'il faut accorder un poids plus important ou au contraire alléger.

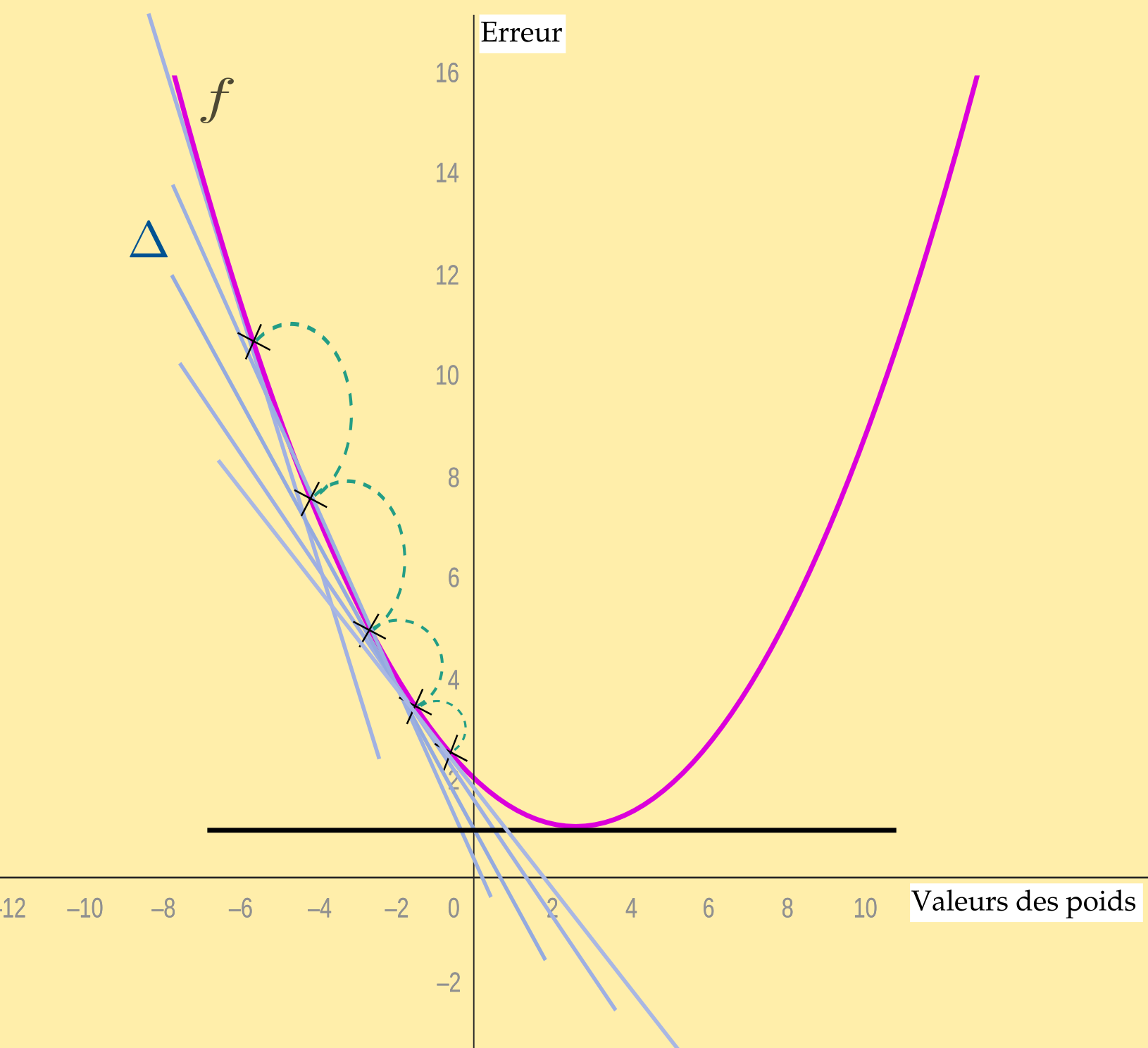
Sur cette coube, on peut calculer des dérivées, c'est-à-dire trouver quel est le comportement local de la fonction, sa tangente (\(\Delta\)). Si vous n'avez pas fait ces maths-là dans un lycée (les tableaux de variations), ce n'est pas très important. Sachez simplement qu'un nombre dérivé donne la mesure de la vitesse (la pente) à laquelle la fonction change selon ses valeurs. Souvenez-vous de la fonction sigmoïde ou de la fonction ReLu citées précédemment, ce sont des autres manières de montrer comment influent les poids sur les valeurs des fonctions neuronales.

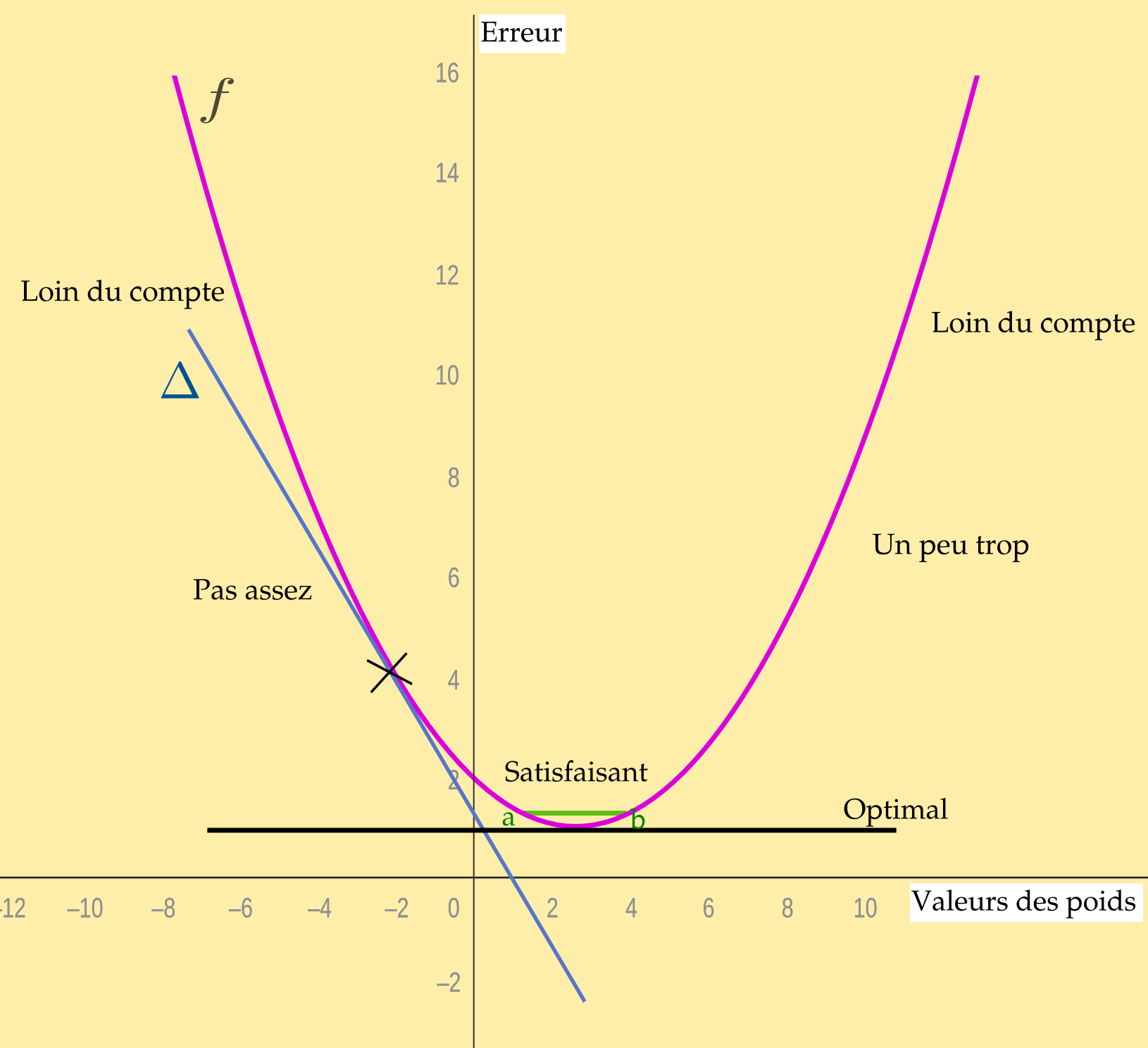
La technique qui consiste à savoir comment se rapprocher le plus du point optimal est une technique... d'optimisation. La plus couramment utilisée en IA est connue sous l'expression de descente de gradient. Pour mieux en comprendre les concepts vous pouvez vous pencher sur les chapitres 8 et 9 de ce livre.

Imaginez que vous descendez la pente d'un côté ou de l'autre de la courbe. Vous allez devoir faire des pas. Si la taille de vos pas est trop grande, une fois que vous serez proche de l'optimum, vous risquez de le dépasser. Si la taille de vos pas est trop petite vous risquez de jamais l'approcher autant que vous le voudriez (ou alors dans mille ans). La taille de vos pas, c'est le taux d'apprentissage.

Notre fonction de perte mesure l'erreur, elle donne les indications pour corriger le poids où l'erreur a été constatée à un instant \(t\) (les croix que vous voyez tracées sur la courbe). On se place dans la position descendante (la tangente dont nous avons parlé ci-dessus) et on fait des pas en essayant d'optimiser leur taille de manière à ce qu'elle soit la plus efficace possible vers l'optimum.

Conclusion

Nous avons commencé avec une étude de cas simple qui nous permet d'expliquer ce qu'est un réseau de neurones en IA. Puis nous avons compliqué notre affaire pour montrer qu'un modèle binaire s'avère insuffisant lorsque nous voulons prendre une décision. Les IA servent à cela : prendre des décisions, à chaque étape du processus où entrent en jeu des valeurs et des poids qui conditionnent l'état du réseau neuronal et aboutissent à un modèle qu'on doit entraîner, affiner, optimiser.

La descente de gradient est un des algorithmes utilisés pour l'apprentissage automatique, il y en a d'autres. Cette explication vous a montré que l'apprentissage automatique s'effectue en utilisant une suite d'algorithmes qui permettent de corriger les connexions au fur et à mesure des itérations successives. Ces « corrections » se font selon un principe de rétropropagation dans le réseau neuronal.

Lorsqu'on fini par aboutir sur un modèle d'IA qu'on juge fiable, l'entraînement et les tests sont terminés. Mais d'autres questions restent en suspend :

quand décide-t-on qu'un modèle est suffisamment entraîné ? lorsqu'on a épuisé tous les jeux de données d'entraînement ? lorsqu'on a enfin réussi à dégager du fond de l'open space l'équipe de matheux qui passent leur temps à affiner les algorithmes d'optimisation ?
dans la mesure où les moyens techniques sont suffisants (puces améliorées, énergie disponible), jusqu'où peut-on aller exactement ? est-ce que l'apparente infinité des améliorations possibles des modèles d'IA est un gage d'efficacité de ces modèles ou est-ce qu'il existe d'autres limites que celles que nous imposent la technologie et l'état des connaissances mathématiques ?