Descente de gradient -- calcul de coût

La phase d'apprentissage d'un modèle d'IA consiste en gros à réduire les erreurs entre le résultat attendu et le résultat réel.

Pour cela il faut utiliser une méthode qui cherche à quantifier l'écart entre ce que prédit le modèle et les valeurs attendues. C'est ce qu'on appelle une fonction de perte ou de coût -- loss function. Il y a plusieurs méthodes selon les systèmes d'IA et les problèmes rencontrés. On peut les classer selon deux grandes catégories, les fonctions de perte de régression et les fonctions de perte de classification. Il faudra alors jouer sur les paramètres (les poids) pour minimiser cette fonction de perte.

Regardons la courbe ci-dessous. Essayons de savoir dans quelle mesure un algorithme de rétropropagation peut permettre d'ajuster les poids, c'est-à-dire les augmenter ou les diminuer. Pour cela il faut procéder par itérations : on entraîne le système de nombreuses fois et on essaye de changer les poids pour voir ce que cela donne. Mais l'algorithme ne sait pas encore dans quel sens il faut aller pour obtenir la valeur optimale. En effet, si on ajuste les poids, on sait que cela change le résultat, mais en mieux ou en moins bien ?

Par contre, il ya une propriété intéressante : si on calcule et trace une tangente à la courbe, on peut en déterminer l'expression d'une fonction dérivée \(f'(x)\). Et on peut alors en déterminer la pente pour toute valeur de \(f(x)\). Ces notions sont très bien expliquées ici.

Dès lors, si on prend un point de la courbe, n'importe lequel, on peut connaître une expression de pente à ce point de \(f'(x)\) et en évaluer la déclivité. Si cette dernière est forte ou faible, c'est qu'on se situe plus ou moins loin de la valeur optimale de \(f(x)\). On procède alors par pas : on effectue la même opération en plusieurs points de la courbe en rapportant l'erreur à la valeur des poids. Un algorithme capable de réaliser ceci se nomme un algorithme de descente de gradient.

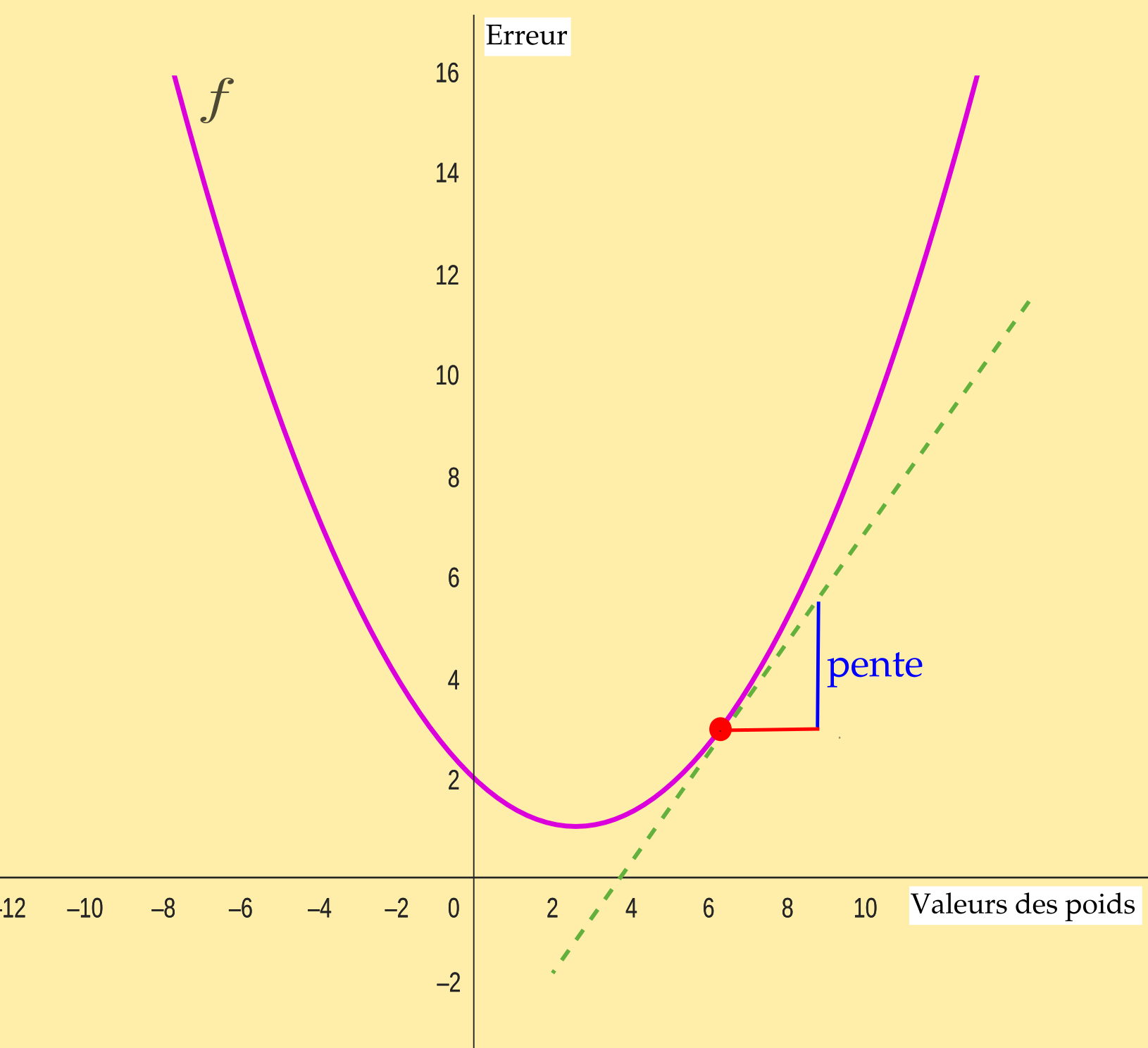
Dans l'image ci-dessus on s'est contenté de prendre une fonction de type \(f(x)=(x-3)^2\). On reste simple mais ne perdez pas de vue que c'est toujours « un peu plus compliqué que cela ».

Pour avancer par pas, ce qui correspond au taux d'apprentissage de l'IA, on avance selon la pente.

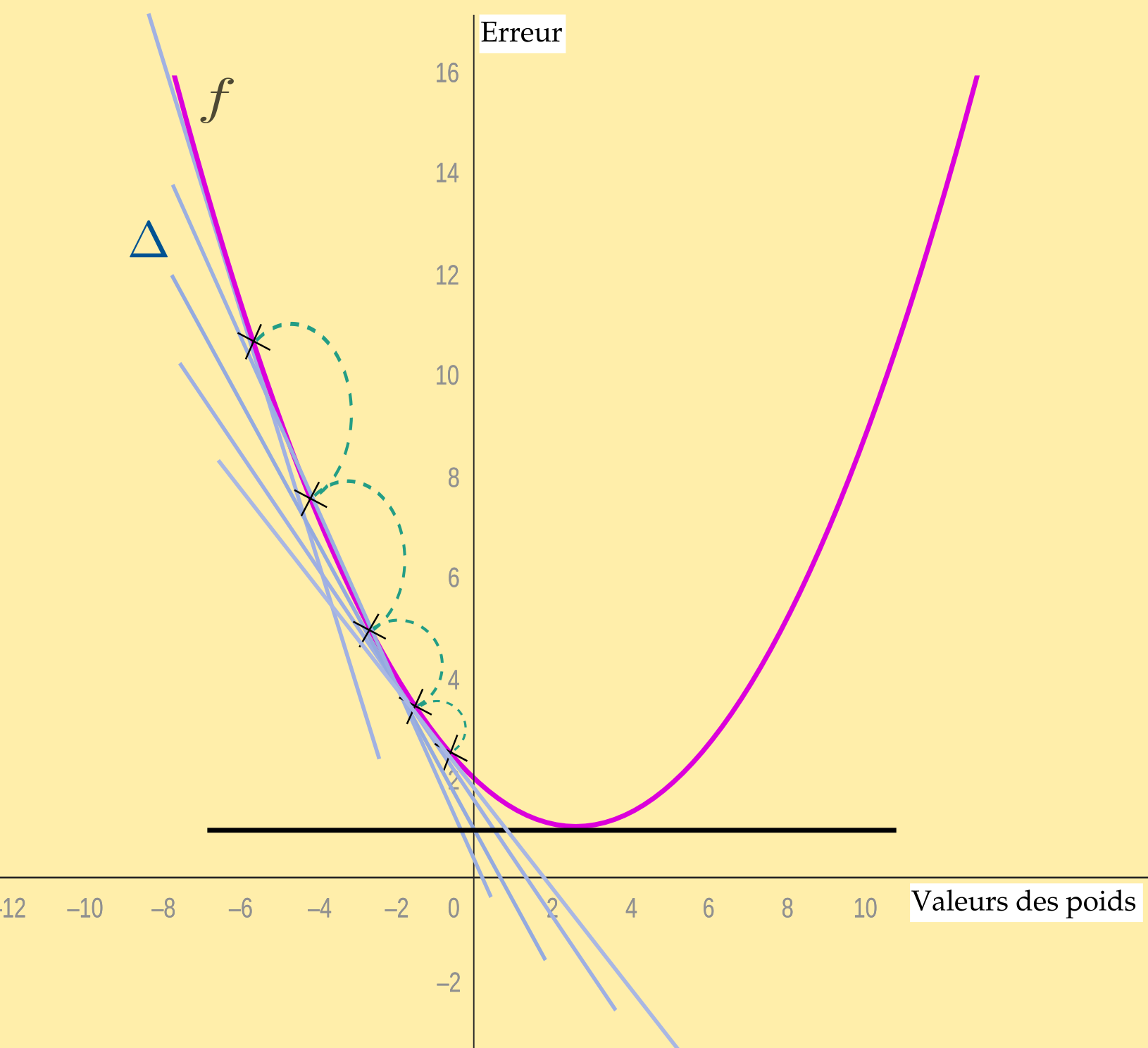
Allons plus en détail pour cette partie de maths

Nous avons donc une fonction de coût (on dit qu'elle est quadratique, au carré) par exemple du type \(J(\theta)=(\theta - 3)^2\).

Le minimum global de cette fonction est donc atteint en \(3\). Il faut y parvenir en ajustant progressivement \(\theta\).

N'oublions pas qu'il faut répéter l'opération pour chaque itération. Il faut donc mettre à jour l'algorithme à chaque fois. La règle pour cette mise à jour de descente de gradient est :

\(\theta_{new}=\theta_{old}-\alpha \times \frac{dJ(\theta)}{d\theta}\)

où :

\(\alpha\) est le taux d'apprentissage (les pas qu'on a vu au dessus)
\(\frac{dJ(\theta)}{d\theta}\) est la dérivée de la fonction de coût par rapport à \(\theta\)

Dans notre cas cette dérivée est :

\(\frac{dJ(\theta)}{d\theta} = 2(\theta - 3)\)

Explications

Ne vous laissez pas avoir par les lettres, il ne s'agit que de conventions.

Souvenez-vous : la dérivée de \(f(x)=(x-3)^2\), c'est \(f'(x)=2(x-3)\).

Parce que...

Dérivation des fonctions composées : on peut considérer la fonction comme

\(u(v(x))\)

avec \(u(x)=x^2\)

et \(v(x)=(x-3)\)

\(u(x)=x^2\) et \(v(x)=(x-3)\)

\(u'(x)=2x\) et \(v'(x)=1\)

\(u'(v(x))=2(x-3)\)

La règle dit:

\((u(v(x))'=u'(v(x)) \times v'(x)\)

\(=2(x-3) \times 1\)

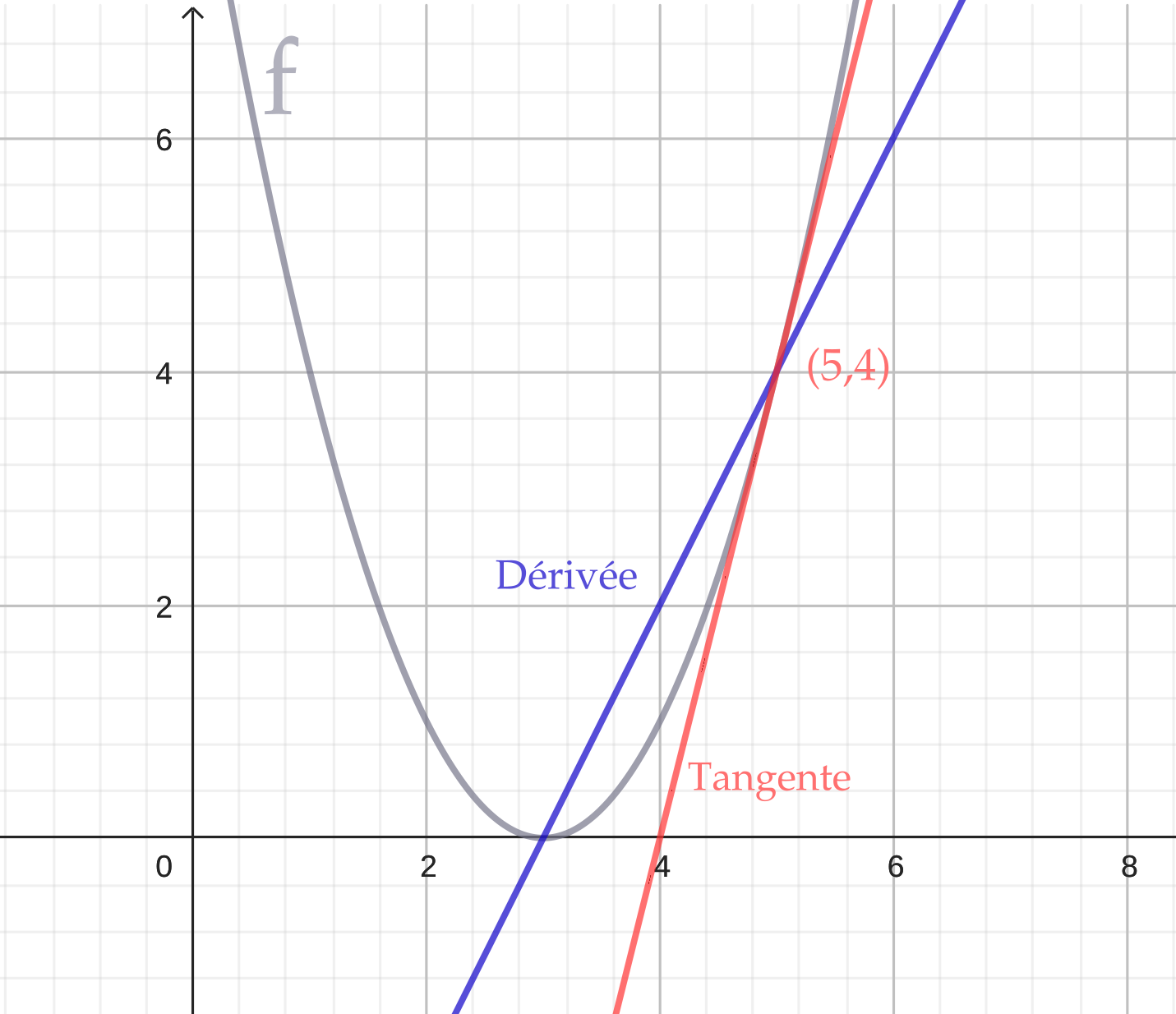
Pour la tengente par exemple en (5,4), remplaçons les \(x\) :

\(f'(5)=2(5-3)=4\)

L'équation de la droite tangente est donc : \(y=4x+b\)

Trouver l'ordonnée à l'origine :

\(4=4 \times 5+b\)

\(b+20=4\)

\(b=-16\)

Équation de la droite tangente : \(y=4x-16\)

Pour résumer, la méthode de descente de gradient présente quatre phases

Initialisation : on commence par choisir des valeurs initiales pour les paramètres du modèle (souvent de manière aléatoire),
Calcul du gradient : On calcule le gradient de la fonction de coût par rapport aux paramètres. Le gradient est un vecteur de dérivées partielles qui indique la direction de la plus forte augmentation de la fonction de coût.
Mise à jour des paramètres : on met à jour les paramètres en suivant la direction opposée au gradient. Cela signifie que l’on descend la pente de la fonction de coût pour trouver un minimum. La mise à jour se fait selon la formule \(\theta = \theta - \alpha \nabla J(\theta)\) où \(\theta\) représente les paramètres, \(\alpha\) est le taux d’apprentissage, et \(\nabla J(\theta)\) est le gradient de la fonction de coût (\(J\)).
Répétition : on répète les étapes 2 et 3 jusqu’à ce que la fonction de coût converge vers un minimum, c’est-à-dire que les changements deviennent très petits ou qu’un nombre prédéfini d’itérations est atteint.

La clé de la descente de gradient est le choix du taux d’apprentissage (\(\alpha\)). S’il est trop grand, on risque de sauter le minimum ; s’il est trop petit, l’algorithme peut être très lent.